
Spatial analysis of stomach and liver cancers in California
Introduction
Cancer is the second leading cause of death, not only in the United States but also worldwide (1,2). Globally, stomach and liver cancers are listed in the most common causes of cancer death (2). In the United States, 35% of the patients who are diagnosed will die from the disease (3). According to the estimates by National Institutes of Health (NIH), in the year 2018, the incidence (the number of new cases) of stomach and liver cancers exceeded 26,000 and 42,000, respectively, while more than 10,000 and 30,000 patients died from stomach and liver cancers, respectively.
California, located in the west coastal region of the United States, is the largest state by population in the United States. It has had the highest rates of new stomach and liver cancers in the country since 1999 and 2004, respectively (1).
We explored impact of ecological risk factors associated with each cancer, including 1,2,3-trichloropropane (TCP) in drinking water, poverty, rurality, gender, and race (4-6). All variables above were measured at county level among 58 counties in California. Due to its intense agricultural use of the land and relaxed prior regulation on the releases of chemicals in the water aquifers, many California counties have been detected to have elevated levels of potent carcinogens in its wells and public water systems (7,8). One of the most toxic chemicals found was TCP, which, based on animal studies, has been shown to be associated with stomach, liver and other cancers in rats (9). No studies have discussed the association between stomach and liver cancers with the variable TCP in California. Among the demographic factors, we estimated the relationships between the area-level variables of percent below poverty level (poverty, %), percent of rural area (rurality, %), percent of males (male, %), and percent of African Americans (AA, %) with the incidence of stomach and liver cancers, respectively. Spatial variations of stomach and liver cancers have been found in some other geographical areas, including Ontario province in Canada, and Shenzhen, a major sub-provincial city in China (10-12), however, to date, spatial distributions of these two cancers have not been explored in California.
The purpose of this study was to assess, via a Bayesian analysis, the spatial distributions of relative rates for stomach and liver cancer and the associations of these diseases with TCP in drinking water, along with poverty, rurality, gender, and race. This county level risk estimation will help identify regions that may need targeted interventions designed to reduce the disease burden.
Methods
Data
Liver and stomach cancer incidence data from the years 2006 to 2015 were obtained from the National Cancer Institute Surveillance, Epidemiology, and End Results Program (SEER) from cancer registries in California (13). SEER is an authoritative source of information on cancer incidence and survival in the United States (14). The data were collected from population-based cancer registries (14). No obvious temporal pattern was detected in preliminary examination of the incidence for both cancers. As aggregating longitudinal data increase the capacity to detect spatial patterns, we included the total incidence in California at county level from the year 2006 to 2015 for each cancer separately. In order to calculate the age standardized incidence ratio (SIR), we considered three age groups: 20–39, 40–59, and 60–79 years. We used California population data from the same years as our outcome, 2006–2015, when calculating SIR. The population data were obtained from the United States Census Bureau (15). Also, several covariates were considered, such as percent of males (male), percent below poverty level (poverty), percent of rural area (rural), percent of African Americans (AA), and percent of TCP over the public health goal (PHG) level (TCP over the maximum allowed level) in each county in California. We assessed the percent of males from SEER (16). The percent of rural area was based on the 2010 census (17). The percent below poverty level and percent of African Americans was obtained from 2011–2015 American Community Survey 5-Year Estimates (15). The TCP test data through 2006–2018 was obtained from the drinking water programs of the California water boards which maintains the drinking water’s quality analyses database (18). Only the active public water system and wells test results were included in our analysis. We used the allowed cutoff-PHG for TCP the cutoff (19). The percent of the allowed TCP was calculated as the percentage of test results in each county beyond established PHG cutoff of 0.0007 µg/L.
Statistical methods
Bayesian approaches offer natural framework for epidemiological studies, where the spatial distribution and determinants relating to health need to be considered (20). Due to the rapid development of computing, Bayesian approaches are now widely used. To reach the goal of disease mapping, spatial models which account for the spatial correlation between adjacent regions using random effects can be considered in the process of making inference. The random effects, including unstructured heterogeneity (UH) and structured heterogeneity (CH), can capture the spatial correlation not explained by the covariates. To capture the spatial correlated heterogeneity, a few models were used, such as the conditional autoregressive (CAR) model (21) and Besag, York and Mollie (BYM) model (22). By allowing each spatial area to have a different coefficient, the model can also be extended in a geographically weighted regression (GWR) setting.
The purpose of this study was to explore the spatial distribution of the relative risk of stomach cancer and liver cancer respectively and related socioeconomic variables in 58 counties of California, USA, incorporating random effects. A Poisson-lognormal model used to fit each cancer type separately is given by:
where yi is the total number of the observed incidence of the stomach cancer or liver cancer considered in county i. θi is the relative risk and Ei is the expected incidence of the cancer considered in county i, which is the product of state incidence rate and county population (Popi). i = 1,...,n, n = 58 is the total number of counties. α is the intercept, and α ~ N(0,0.005−2) distribution.
βj is the coefficient for jth covariate, βj ~ N(0,0.005−2). The model was also extended in a geographically weighted regression (GWR) setting that local coefficients, βij represents the coefficient of jth covariate for ith county, were estimated by introducing the neighboring features. , where and τω~ Gamma (0.001,0.005). The random effect for the spatially correlated heterogeneity (CH), vi, was assumed to follow a CAR prior:
Where δi represents the neighbor set in the ith county, represents the number of neighbors in the ith county and τv is a hyperparameter, where τv ~ Gamma (0.001,0.005). ui is the random effect for the uncorrelated spatial heterogeneity (UH), , where τu ~ Gamma (0.001,0.005). Separate models were fit for each type of cancer.
We performed sensitivity analyses and the results are robust for different specifications of the prior distribution parameters, for example Gamma (0.001,0.001) and Gamma (1,1) for τv and τu, respectively.
Model selection
To measure the predictive accuracy of the fitted models, we considered the Watanabe Akaike information criterion (WAIC) (23). WAIC is a fully Bayesian measurement (24) for estimating the out-of-sample expectation (25). The computation of WAIC starts with the computed log pointwise predictive density and then subtracts a correction for the numbers of effective parameters (26). The parameters degrees of freedom indicate the complexity of the model. As the deviance information criteria (DIC) is widely used in recent years, it was also included in the results for the purpose of comparison. A lower WAIC/DIC value indicates a better goodness-of-fit.
Computational approach and software
Integrated nested Laplace approximation (INLA) is a Bayesian inference approach proposed by Rue et al. (27) in latent Gaussian models via Laplace approximation. As an alternative of the traditional Bayesian analysis approach which uses Markov chain Monte Carlo (MCMC algorithms), INLA gains a much higher computation speed and accurate estimates (28). R-INLA is an ongoing development R package which provides a user-friendly interface, allowing users to perform inference based on the INLA method (29) through R command. Data preparation work was performed by using SAS version 9.4 (SAS Institute Inc., Cary, NC, USA) and R software (30). The Bayesian analysis was implemented by the R-INLA R package. The graphical displays were using the R software (30).
Results
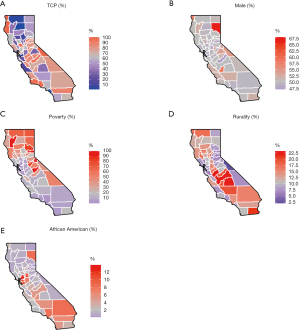
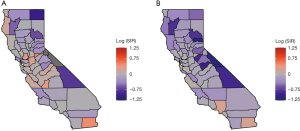
The Figure 1A-1E presents the spatial variation of the variables considered in California, including for TCP (range: 1–100%), percent of male (range: 47–68%), percent of poverty (range: 2–23%), percent of rurality (range: 0–45%), and percent of African American (range: 0–14%). The spatial variations of these variables look different to each other according to the maps. The Figure 2A,2B present the raw log SIR of the stomach and liver cancers respectively. The darker shades in the maps indicate higher SIR. The ranges of log SIR for stomach and liver cancer are (−µ, 0.51] and [−1.11, 0.23], respectively. For the SIR of stomach cancer, the SIR for 20 out of 58 counties was over 0, while for liver cancer it was 9 out of 58 counties. The counties with higher risk are located in the midwestern regions of the state for liver cancer.
Tables 1,2 include the measurements of goodness-of-fit for stomach and liver cancers, respectively. Models 1(a) and (b), 4(a) and (b), and 9(a) and (b) are the models without random effect. The remaining models were based on the spatial model with different random effects and covariates, either with or without geographically weighted regression (GWR). For all models with random effects, there are no major qualitative differences between DIC and WAIC, suggesting that both measurements are appropriate for using when comparing models. Models 1(a) and 1(b), 2(a) and 2(b), 3(a) and 3(b), are models with no covariates. Among all the models considered for stomach cancer, model 12(a) and model 13(a) are the two models have the lowest WAIC values. Due to the model complexity, we chose model 12(a) (percent below poverty level, percent of rural area, and percent of the allowed TCP, UH + CH effects, without GWR) as the best model. For the same reason, among all the models considered for liver cancer, model 10(b) (percent below poverty level, percent of rural area, percent of the allowed TCP, UH effect only, without GWR) was selected. For the models selected, model 12(a) for stomach cancer and model 10(b) for liver cancer, the DIC and WAICs are both smaller than model 2(a) and (b), and model 3(a) and (b), which are the models without covariates, but with UH or UH+CH random effects.
Table 1
| Model | Variables considered | Model names | WAIC | WpD | DIC | pD |
|---|---|---|---|---|---|---|
| Model 1 (a) | No covariates | No random effect | 1,225.83 | 113.31 | 1,089.63 | 1.12 |
| Model 2 (a) | No covariates | UH | 456.85 | 23.21 | 462.39 | 36.85 |
| Model 3 (a) | No covariates | UH + CH | 451.47 | 21.02 | 459.16 | 35.87 |
| Model 4 (a) | All covariates | No random effect | 901.9 | 101.79 | 778.7 | 6.091 |
| Model 5 (a) | All covariates | UH | 447.78 | 20.06 | 453.78 | 32.88 |
| Model 6 (a) | All covariates | UH+GWR | 457.66 | 22.29 | 460.7 | 32.75 |
| Model 7 (a) | All covariates | UH + CH | 447.63 | 19.47 | 452.18 | 30.52 |
| Model 8 (a) | All covariates | UH + CH + GWR | 454.38 | 31.92 | 448.518 | 19.56 |
| Model 9 (a) | Poverty (%) + rural (%) + TCP (%) | No random effect | 905.82 | 92.52 | 793.05 | 4.102 |
| Model 10 (a) | Poverty (%) + rural (%) + TCP (%) | UH | 448.43 | 20.11 | 453.82 | 32.28 |
| Model 11 (a) | Poverty (%) + rural (%) + TCP (%) | UH + GWR | 449.7 | 20.4 | 455.51 | 33.1 |
| Model 12 (a) | Poverty (%) + rural (%) + TCP (%) | UH + CH | 445.96 | 19.26 | 452.99 | 32.75 |
| Model 13 (a) | Poverty (%) + rural (%) +TCP (%) | UH + CH + GWR | 445.64 | 19.16 | 454 | 33.93 |
All covariates include 1,2,3-trichloropropane (TCP) in drinking water (%), poverty in percent (%), rurality (%), gender (%), and race (%). UH, uncorrelated random effects; CH, spatially correlated random effects; GWR, geographically weighted regression.
Table 2
| Model | Variables considered | Model name | WAIC | WpD | DIC | pD |
|---|---|---|---|---|---|---|
| Model 1 (b) | No covariates | No random effect | 1,283.44 | 28.42 | 1,254.95 | 1.16 |
| Model 2 (b) | No covariates | UH | 490.49 | 25.71 | 499.53 | 43.81 |
| Model 3 (b) | No covariates | UH + CH | 490.15 | 25.13 | 499.32 | 43.08 |
| Model 4 (b) | All covariates | No random effect | 1,257.47 | 138.87 | 1,097.58 | 6.13 |
| Model 5 (b) | All covariates | UH | 487.13 | 24.92 | 496.78 | 43.35 |
| Model 6 (b) | All covariates | UH + GWR | 488.8 | 26.09 | 495.67 | 42.12 |
| Model 7 (b) | All covariates | UH + CH | 492.98 | 25.47 | 497.31 | 38.53 |
| Model 8 (b) | All covariates | UH + CH + GWR | 491.22 | 24.97 | 497.53 | 39.9 |
| Model 9 (b) | Poverty (%) + rural (%) + TCP (%) | No random effect | 1,354.14 | 125.87 | 1,213.09 | 4.14 |
| Model 10 (b) | Poverty (%) + rural (%) + TCP (%) | UH | 486.45 | 24.8 | 496.18 | 43.28 |
| Model 11 (b) | Poverty (%) + rural (%) + TCP (%) | UH + GWR | 488.46 | 26.13 | 495.38 | 42.28 |
| Model 12 (b) | Poverty (%) + rural (%) + TCP (%) | UH + CH | 488.35 | 24.84 | 495.92 | 41.06 |
| Model 13 (b) | Poverty (%) + rural (%) + TCP (%) | UH + CH + GWR | 487.56 | 24.59 | 496.28 | 41.9 |
All covariates include 1,2,3-trichloropropane (TCP) in drinking water (%), poverty in percent (%), rurality (%), gender (%), and race (%). UH, uncorrelated random effects; CH, spatially correlated random effects; GWR, geographically weighted regression.
Tables 3,4 include the posterior results for the parameter estimates of model 12(a) and model 10(b). For both stomach and liver cancers, the percent of rural area and percent below poverty level were significant determinants. Specifically, according to model 12(a), one unit increase of the percent of poverty increased the relative risk of stomach cancer by 1.3% (95% CI: 0.4−2.1%); one unit increase of the percent of rural area decreased the relative risk of stomach cancer by 0.5% (95% CI: 0.2−0.7%). And, according to model 10(b), one unit increase of the percent of poverty increased the relative risk of stomach cancer by 1.5% (95% CI: 0.4−2.6%); one unit increase of the percent of rural area decreased the relative risk of stomach cancer by 0.2% (95% CI: 0.1−0.5%). However, we did not find any association between percent of the allowed TCP for either cancer type.
Table 3
| Variables | UH + CH model | |
|---|---|---|
| Mean (std dev) | 95% CI | |
| Intercept | 0.808 (0.058) | 0.697–0.926* |
| Poverty (%) | 1.013 (0.004) | 1.004–1.021* |
| Rural (%) | 0.995 (0.001) | 0.993–0.998* |
| TCP (%) | 0.984 (0.070) | 0.854–1.129 |
*, indicates that 1 does not belong to the 95% CI.
Table 4
| Variables | UH model | |
|---|---|---|
| Mean (std dev) | 95% CI | |
| Intercept | 0.806 (0.075) | 0.664–0.961* |
| Poverty (%) | 1.015 (0.006) | 1.004–1.026* |
| Rural (%) | 0.998 (0.001) | 0.995–0.999* |
| TCP (%) | 1.108 (0.102) | 0.921–1.319 |
*, indicates that 1 does not belong to the 95% CI.
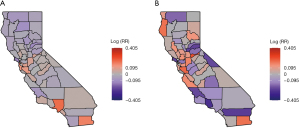
Figure 3A displays the log relative risk (uncorrelated and spatially correlated heterogeneity (UH + CH) random effects) estimated in model 12(a), and Figure 3B includes the log relative risk [the uncorrelated heterogeneity (UH) random effects] estimated in model 10(b). Both maps present a variability of the distribution of stomach and liver cancers in California. The map of liver cancer shows a higher variability when compared with the map of stomach cancer. For stomach cancer, the estimated log relative risk was between −0.13 and 0.27. Among them, 24 out of 58 counties had a log relative risk greater than 0. For liver cancer, the estimated log relative risk ranged between −0.27 and 0.60. Among them, 29 out of 58 counties had a log relative risk greater than 0. Figure 4A,4B provides the map of probability of log RR greater than 0 estimated by model 12(a), and the map of the probability that the estimated log(RR) >0 estimated by model 10(b). The orange, grey, and purple colors visualize these probabilities in categories of greater than 0.5, around 0.5, and less than 0.5. For stomach cancer, a small cluster of excess risk was located in the mid-west region. For liver cancer, the counties with higher liver cancer relative risk were clustered from the mid-west (Bay area) to northwestern region. In addition, for both stomach and liver cancers, the excess risk was also found in Imperial county located in the southmost county.

Discussion
In our spatial Bayesian analysis, models with random effects greatly outperformed the models without random effects. There was a marked spatial variation of liver cancers in California at the county level. Also, we have found lower risk for each cancer type associated with rural regions, and an increased risk associated with poverty. Our findings agree with the results from other studies. For example, in 2003, Horton discussed the socioeconomic factors, including poverty and rurality with cancers, such as stomach and liver cancers (31). He concluded that less developed societies tend to have higher cancer incidence. Also, Kogevinas et al. in 1997 pointed out that in the lower social strata, excess risks were found in both stomach and liver cancers (32). In other studies, both cancers were found to be more common in males than in females (3,33). Also, among other races and ethnicities, the two cancers were found to be the least prevalent among non-Hispanic Whites (3,33). However, we have not found any association related to sex and ethnicities.
Limitations of our project includes the fact that the data used for TCP were not a random sample and instead based on the available tests during the time periods considered. The TCP data were collected based on the regular monitoring of drinking water chemicals by California water boards. Each community water system is required to collect four quarterly samples during the designated year prior to any treatment. The designated year is based on historical monitoring frequency and laboratory capacity by the state water board (34). Also, the presence of TCP above the allowed level does not necessarily mean the water was used as drinking water. Both the continuous TCP data and percent of the allowed TCP were considered, but no association result was found. Also, due to confidentiality, individual data was not available, and the data was aggregated at the county level. As a shortfall of ecological study, there is a loss of information due to aggregation. Therefore, further studies should examine the reasons for the association between poverty and rurality between stomach and liver cancers. A limitation in the modeling is that instead of age adjusted expected incidence, general expected incidence was used.
Our findings could help public health officials identify regions with higher cancer relative risk, and better understand the risk factors for these diseases, such as spatial location, poverty and rurality. This can help public health administrators more appropriately plan and target the use of available resources to reduce the burden in the high risk areas. Suggestions include motivating screening for established risk factors and prevention activities and increasing the public awareness of stomach and liver cancers in high risk areas.
Acknowledgments
Funding: This work was funded by the College of Art and Science, Western Michigan University.
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Peter Baade, Susanna Cramb) for the series “Spatial Patterns in Cancer Epidemiology” published in Annals of Cancer Epidemiology. The article has undergone external peer review.
Conflicts of Interest: Both authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/ace-19-21). The series “Spatial Patterns in Cancer Epidemiology” was commissioned by the editorial office without any funding or sponsorship. The authors report that this work was funded by the college of Art and Science, Western Michigan University. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The project does not include human subject research since we used aggregated data at the county level. No ethnics approval is required.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Centers for Disease Control and Prevention. United states cancer statistics: Data visualizations. Available online: https://gis.cdc.gov/Cancer/USCS/DataViz.html 2018. Accessed July 24, 2018.
- World Health Organization. World Health Cancer. Available online: http://www.who.int/news-room/fact-sheets/detail/cancer 2018. Accessed: July 24, 2018.
- National Cancer Institute Cancer statistics. Available online: https://www.cancer.gov/about-cancer/understanding/statistics 2018. Accessed August 1, 2018.
- The American Cancer Society medical and editorial content team. Liver Cancer Risk Factors. Available online: https://www.cancer.org/content/dam/CRC/PDF/Public/8699.00.pdf 2021. Accessed July 18, 2021.
- The American Cancer Society medical and editorial content team. Stomach Cancer Risk Factors. Available online: https://www.cancer.org/content/dam/CRC/PDF/Public/8839.00.pdf 2021. Accessed July 18, 2021.
- Walker B Cancer-Causing Pesticide ‘Garbage’ Taints Tap Water for Millions in California. Available online: https://www.ewg.org/research/cancer-causing-pesticide-garbage-taints-tap-water-millions-california 2017. Accessed July 18, 2021.
- Evans S, Campbell C, Naidenko OV. Cumulative risk analysis of carcinogenic contaminants in United States drinking water. Heliyon 2019;5:e02314 [Crossref] [PubMed]
- Harris-Lovett SR, Binz C, Sedlak DL, et al. Beyond User Acceptance: A Legitimacy Framework for Potable Water Reuse in California. Environ Sci Technol 2015;49:7552-61. [Crossref] [PubMed]
- National Toxicology Program. NTP Toxicology and Carcinogenesis of 1,2,3-Trichloropropane (CAS No. 96-18-4) in F344/N Rats and B6C3F1 Mice (Gavage Studies). Natl Toxicol Program Tech Rep Ser 1993;384:1-348. [PubMed]
- Van Leeuwen JA, Waltner-Toews D, Abernathy T, et al. Associations between stomach cancer incidence and drinking water contamination with atrazine and nitrate in Ontario (Canada) agroecosystems, 1987-1991. Int J Epidemiol 1999;28:836-40. [Crossref] [PubMed]
- Chen Y, Yi Q, Mao Y. Cluster of liver cancer and immigration: a geographic analysis of incidence data for Ontario 1998-2002. Int J Health Geogr 2008;7:28. [Crossref] [PubMed]
- Weng M, Pi J, Tan B, et al. Area deprivation and liver cancer prevalence in Shenzhen, China: A spatial approach based on social indicators. Social Indicators Research 2017;133:317-32. [Crossref]
- NCI's Division of Cancer Control and Population Sciences. National Cancer Institute Cancer stat facts: Liver and intrahepatic bile duct cancer. Available online: https://seer.cancer.gov/statfacts/html/livibd.html 2018. Accessed July 31, 2018.
- NCI's Division of Cancer Control and Population Sciences. National Cancer Institute Overview of the seer program. Available online: https://seer.cancer.gov/about/overview.html 2018. Accessed July 24, 2018.
- United States Census Bureau. 2011-2015 American Community Survey (2013) /American Fact Finder. “S1702: poverty status in the past 12 months of families”. Available online: http://factfinder2.census.gov 2013. Accessed May 10, 2018.
- Surveillance, Epidemiology, and End Results (SEER) Program (www.seercancer.gov). Database: Incidence - seer 9 regs research data, Nov 2017 sub (1973-2015) population adjustment - linked to county attributes - total U.S., 1969-2016 counties, national cancer institute, surveillance research program. Available online: https://seer.cancer.gov/data/access.html 2018. Accessed April, 2018.
- US Census Bureau. 2010 Census. American Fact Finder. “URBAN AND RURAL”. Available online: http://factfinder2.census.gov 2010. Accessed June 5, 2018.
- California State Water Resources Control Board. Edt library and water quality analyses data and download page. Available online: https://www.waterboards.ca.gov/drinking_water/certlic/drinkingwater/EDTlibrary.html 2018. Accessed July 24, 2018.
- Office of Environmental Health Hazard Assessment, California Environmental Protection Agency. Public health goals (PHGS). Available online: https://oehha.ca.gov/water/public-health-goals-phgs 2018. Accessed August 1, 2018.
- Ashby D, Hutton JL. Bayesian epidemiology. Statistics Textbooks and Monographs 1996;151:109-40.
- Besag J, York J, Mollie A. Bayesian image restoration, with two applications in spatial statistics. Ann Inst Stat Math 1991;43:1-59. [Crossref]
- Knorr-Held L, Besag J. Modelling risk from a disease in time and space. Stat Med 1998;17:2045-60. [Crossref] [PubMed]
- Watanabe S. Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J Mach Learn Re 2010;11:3571-94.
- Vehtari A, Gelman A. Deviance information criterion (DIC). Available online: https://arxiv.org/abs/1307.5928 2016. Accessed August 28, 2021.
- Akaike H. Information theory and an extension of the maximum likelihood principle. In: Selected papers of Hirotugu Akaike. Springer, 1998:199-213.
- Gelman A, Hwang J, Vehtari A. Understanding predictive information criteria for Bayesian models. Statistics and Computing 2014;24:997-1016. [Crossref]
- Rue H, Martino S, Chopin N. Approximate Bayesian inference for latent gaussian models by using integrated nested Laplace approximations. J R Stat Soc Series B Stat Method 2009;71:319-392. [Crossref]
- Martino S, Rue H. Implementing approximate Bayesian inference using integrated nested Laplace approximation: A manual for the INLA program. Department of Mathematical Sciences, NTNU, Norway 2009.
- Martins TG, Simpson D, Lindgren F, et al. Bayesian computing with INLA: new features. Computational Statistics & Data Analysis 2013;67:68-83. [Crossref]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Available online: https://www.R-project.org/ 2018.
- Horton R. Medical journals: evidence of bias against the diseases of poverty. Lancet 2003;361:712-3. [Crossref] [PubMed]
- Kogevinas M, Porta M. Socioeconomic Differences in Cancer Survival: A Review of the Evidence. In: Kogevinas N, Pearce N, Susser M, et al. editors. International Agency for Research on Cancer. Scientific Publications 1997;137:178-82.
- National Cancer Institute. Cancer stat facts: Stomach cancer. Available online: https://seer.cancer.gov/statfacts/html/stomach.html 2018. Accessed July 31, 2018.
- The State Boards Division of Drinking Water of California. California regulations related to drinking water. Available online: https://www.waterboards.ca.gov/drinking_water/certlic/drinkingwater/documents/lawbook/DW-regulations-2018-04-10.pdf 2015. Accessed August 30, 2018.
Cite this article as: Fisher G, Shen Y. Spatial analysis of stomach and liver cancers in California. Ann Cancer Epidemiol 2021;5:5.


