Bayesian modeling of georeferenced cancer survival
Introduction
Survival analysis is an old subfield of statistics, dating back to the development of life tables (1). The use of spatial survival methods in cancer research has become more widespread due to the increased recognition of the association between the spatial location and health outcomes, increased availability of spatial data and improvements in computing power. Health initiatives, such as Healthy People 2020 in the United States (2) and the World Health Organization Health Equity Monitor (3) aim to eliminate cancer health disparities, such as those due to geographical location.
The predictors, such as racial composition (4) and socio-economic status (5) can also have a geographical influence on survival (6).
Investigating spatial variations in survival patterns is important since it provides evidence to identify areas with poorer cancer outcomes requiring attention, thus assisting public health professionals in their decision making. The geographical location can be used as a surrogate for environmental or lifestyle factors that may influence population cancer survival. Bayesian approaches are increasingly commonly used for modelling small area spatial survival data. Advantages of Bayesian models in comparison to other methods include the ease of drawing strength from neighboring regions, usually via spatially correlated or uncorrelated random effects. Also, Bayesian methods enable the development of more complex models, inferences and analyses.
In this paper we provide an overview of the fundamental and more advanced Bayesian spatial survival methodologies that can be applied to cancer research. The paper is structured as follows. In section 2, we describe some fundamental survival analysis concepts. In section 3, we introduce current Bayesian models that describe the spatial variation in survival, such as using random effects (subsection 3.1), cure-rates (subsection 3.2) and direct spatial models (subsection 3.3). In section 4, we discuss various software for spatial survival analysis. Section 5 includes a case study for a spatial survival model with random effects using the Louisiana prostate cancer Surveillance, Epidemiology and End Results (SEER) data from the United States (7). In section 6 we present some conclusion.
Fundamentals of survival analysis
Survival analysis refers to the analysis of the time taken for a particular event to occur. This form of analysis attempts to describe the distribution of the survival time and understand differences in the survival time, perhaps due to demographics, risk factors or spatial location. Both the time of origin and the event of interest must be precisely specified, so that the length of time from the origin to the endpoint can be calculated. For example, for cancer patients, the origin could be time of cancer diagnosis and the endpoint could be death due to the particular cancer studied. Another example would be the point of origin being the start of cancer treatment and the endpoint being cancer recurrence.
Survival can be described in terms of the survival function, the hazard function or the likelihood. We first describe how these functions relate to each other and then we discuss the distributions that may be used.
Let T denote the random variable representing the time to event. The cumulative distribution function of T, denoted F(t), is defined as F(t) = P(T ≤ t), which is an increasing function of t, ranging from 0 to 1. The survival function S(t) is defined as the probability of survival up to time t, S(t) = P(T > t) = 1− F(t), which is a decreasing function ranging from 1 to 0. The probability density function is defined as:
The cumulative density functions and survival functions can be expressed in terms of the probability distribution function as follows:
The hazard function represents the instantaneous probability of having an event at time t, given that one has survived up to time t. In particular,
where is approximately the conditional probability that the event occurs within the interval [t, t +δ] given that the event has not occurred before time t.
The hazard function can also be expressed as a function of the survival function as follows:
Conversely, the cumulative hazard function is related to the survival function as follows: .
Common choices for the distribution of time to endpoint are among the Weibull or extreme value, lognormal or gamma families of distributions. Hence a basic parametric survival data model consists of an endpoint distribution, such as the exponential, Weibull and Pareto distributions, and the nature of the survival experience is modelled via assumptions about the parameters of that distribution.
The Weibull distribution is commonly used for time to event data since it can model a decreasing, constant or increasing failure rate over time, if its shape parameter μ is less than, equal to or greater than 1 respectively. The exponential distribution is a special case of the Weibull distribution, where the shape parameter is 1.
The probability of an endpoint at time ti under the Weibull distribution is specified by:
The survival and hazard functions derived from this are:
This allows a straightforward specification of the model components for this distribution:
Covariates and random effects can be included within λ and the parameter μ provides the shape of the distribution as it will be discussed in greater detail below.
A particular complexity of survival data is censoring, which usually occurs when the survival times are not known precisely, but are known to fall within a certain time interval. Censoring can arise from patient drop out, loss to follow up and competing risks, such as deaths from other causes. Right, left and interval censoring occur when the lower limit, upper limit or an interval only are known for the true event times, respectively.
Survival analysis methods can be extended to adjust for several risk factors. Weibull regression is one of the most popular parametric regression techniques. It assumes a Weibull distribution for the density of survival times, and allows the covariates to be fit linearly on the log of its scale parameter. A more general form is the accelerated failure time models (AFT), in which log(T) is modeled as a linear function of the covariates plus an error term. In AFT models, the survival times are assumed to have a Weibull, log logistic or log normal distribution.
Another popular regression technique for survival analysis is the Cox proportional hazard model, which estimates the hazard rate, assuming a constant hazard ratio over time. In this model, the hazard is a product of a baseline hazard and an exponential function of a linear combination of predictors. This model does not impose a parametric form on the survival times. This model is expressed by the hazard function as follows:
where t represents the survival times, is the hazard function, are the coefficients measuring the effects of the covariates, is the baseline hazard when all the covariates are zero. The model assumes a constant hazard ratio over time. The exponentiated coefficients, are called hazard ratios. A hazard ratio greater than 1 indicates that, as the covariate increases, the event hazard increases, and therefore the length of survival decreases.
For a more detailed review of fundamental survival analysis models using frequentist approaches, see Kleinbaum and Klein (8). Reviews of Bayesian survival methods can be found in Gustavson (9), Ibrahaim et al. (10) and Banerjee (11).
Including spatial effects in survival models
Random effects models
Often location data are often available at a regional level (county, census tract, or zip code). “Spatial survival models include random effects to help account for the spatial variability in survival. Usually, each region in the study area represents a level of the random effect and the effect for each level is drawn from a distribution. The random effects are added to the linear predictor component of the model. Random effects may account for spatially correlated and uncorrelated effects. Spatial correlations occur when neighboring regions have similar outcomes. Spatially uncorrelated random effects are independent of neighboring regions. The mean of the random variable is therefore constrained to zero to avoid identifiability problems. Therefore, the uncorrelated random effect is modeled using a Normal prior with mean 0 and variance , .
Spatially correlated random effects can be employed to account for spatial dependency. Several models exist to describe the spatial dependencies. Besag et al. (12) proposed an intrinsic autoregressive model, often referred to as the conditional autoregressive (CAR) model (13), where the spatial effect of a particular region depends on the effects of neighboring regions. The random effect is the spatially structured random effect, assumed to have a CAR distribution:
where is the number of neighboring counties who share boundaries with the one, and is the variance parameter for the spatially structured effect. The random effects are added to the linear predictor component of the model. For example, in the context of a Weibull survival model, assuming a Weibull (μ, λi) distribution for the survival times, the covariates and spatial random effects are linked to the log(λi) parameter as follows:
where i represents the individual, j represents the county, β0 is the intercept, is the vector of regression parameters, p is the number of covariates and is a vector of covariates, is the uncorrelated random effect and is the spatially correlated random effect.
The convolution model, also known as the Besag, York and Molié (BYM) model (13,14) includes both uncorrelated and spatially correlated random effects.”
Spatial survival methods with random effects have been used for various cancers, such as prostate cancer (15,16) leukemia (17), breast cancer (18,19), and cancer control (20).
Cure rates
One of the assumptions in the standard survival models is that all the subjects die from the cancer of interest and all individuals who do not experience the event are considered censored. The fact that for some cancer types, the death rates may approach normal rates after a certain period of time, led to the development of cure rate models (21), which assume that a certain fraction of the cancerous population are considered cured from cancer, while the rest are considered noncured.
The most popular cure rate model is the mixture model (21), which assumes that the population consists of a group that will be cured from the disease of interest and a group of non-cured individuals. Although the mixture cure-rates model is able to provide estimates for both the proportion of subjects who are cured and the survival function for the uncured subjects, caution is needed since the estimation of the cure rate fraction can be dependent on the length of follow-up time and parameters may not be identifiable for some datasets (22). It has also been shown that some subjects may experience the same death rates as the general population, however they have higher death rates from the cancer of interest and lower rates from other causes. This is the case for subjects from higher socio-economic classes who have a higher rate of breast cancer but lower rate of other diseases (23). Possible solutions to these issues include the use of cause specific deaths, examination of the likelihood function and including a sufficiently large population and follow-up time. In addition, understanding the biological mechanisms that lead to disease manifestation may provide information on the appropriateness of the model assumptions used. If p is the probability of being cured, then the population survival function is calculated as a mixture S(t) = p+(1-p)S0(t)., where S0(t)=P(T>t) is the survivor function in the noncured group and T is the lifetime of the individual. These models can be fitted with covariates, allowing them to explain the survival of noncured subjects or the probability of being cured or both.
There is a growing literature on the development of spatial survival models using cure rates, mostly developed by including the spatial heterogeneity via uncorrelated and spatially correlated random effects, such as those applied to colon cancer (24) or smoking cessation (25). Rua and Dey (26) developed a class of hierarchical Bayesian models for spatially or spatio-temporal data integrating cure rates and spatio-temporal random effects and having the proportional hazards and proportional odds models as special cases. The methodology is illustrated using melanoma cancer data from the Surveillance, Epidemiology and End Results SEER database. A second class of cure rate models originates from the cancer model developed by Yakovlev (27) and takes into consideration the underlying processes of disease manifestations, assuming that a subject is at risk of failure only after exposure to some latent risks, otherwise being considered cured (28). More recent developments extend these cure rate models for spatially correlated survival data including both spatially correlated and uncorrelated random effects. Li et al. (29) used SEER colon cancer data and employed a generalized extreme value distribution on the survival time, modeling nonlinear covariate effects on the cure rate and considering the spatial variations. A unifying general class of cure rate models which includes the standard mixture and latent factor cure rates model as special cased was developed by Cooner et al. (30). This general model has also been used in a Bayesian framework for county level aggregated data enabling flexible modeling of spatial associations using a univariate or bivariate latent spatial cure rate model (31). This spatial model has been applied to breast cancer data from the SEER registry in Iowa, the results suggesting differential survival experience for various regions.
In modeling the spatial variation in cure rate models using random effects, there are several choices that can be made. One can assume that the cure fractions are spatially associated or alternatively, the spatial variability can be considered in the model regressors. Models with spatial random effects in both components can also be considered, provided such effects are estimable (31). The cure rate models can been used to model recurrent events which are frequent for cancer data, such as recurrences after breast cancer (32) or leukemia recurrence (33). Extension to a spatial cure rate multivariate survival model has been proposed and applied to prostate cancer data (15). The multivariate models can be applied to jointly model several time-to-event variables, such as time of cancer relapse to various organs or time to cancer relapse and time to death.
Direct spatial models
Although widely used for spatial survival models, random effects are limited in their interpretability due to their wide range on the real line. Usually, higher random effects for an area are an indication of an increased risk, and can be interpreted in comparison with each other to highlight areas of higher risk, but they are not a direct estimate of the risk in the area. Alternative models for spatial survival have been proposed using spatially explicit survival models, with application to prostate cancer data from the SEER registry (22,34-36). The definition of the survival, density and hazard functions can be broadened by explicitly modeling the spatial dependency using direct derivations of these functions and their marginals and conditionals as proposed in Onicescu and Lawson (36).
The spatially explicit survival for area AS at time t* can be defined as , where s is a spatial location defined by latitude and longitude, and t is the time.
Assuming independence between space and time, the space-time probability distribution function can be defined as the product between the temporal and spatial distribution functions. The temporal component probability density function can be assumed to have a distribution suitable for time to event data, such as the Weibull distribution (23). For specifying the spatial distribution, one needs to define the spatial dependence structure, which is of fundamental importance to all spatially referenced data. There are a wide variety of choices that can be used to specify the spatial model. One approach is to assume a geostatistical model whereby the spatial component is assumed to follow a Gaussian process with spatial dependence defined by a covariance function, usually assumed to be second order stationary, with the covariance between any two locations depending on the distance between them (37). However, spatial modeling using the covariance function is computationally restrictive due to the necessity for inversion of a potentially large positive definite matrix. One alternative to directly specifying the covariance function is to assume a process convolution model (38), which is based on the idea that any stationary Gaussian process can be expressed as the convolution of a white noise process with a specified kernel . The advantage of the convolution based models lies in their computational simplicity. In addition, they always induce valid covariance functions and, due to their nonparametric nature, have considerable flexibility versus a fully parametric approach. As described in Higdon et al. (38), the model for the spatial process is determined by specifying the white noise process and the smoothing kernel. For approximate calculations, a fixed number of grid points are generated over the polygon region. A common choice for the smoothing kernel is the Gaussian kernel, since it induces a covariance matrix which is a function of the squared distance between two spatial locations and gradually dies off with increased distance. The Gaussian process can be constructed over a spatial region as the weighted average over the grid points in the region of the white noise process and the gaussian kernel (38). Alternative formulations have been used for aggregated data by using the centroid location for each region (36).
The spatial explicit model has also been used assuming an accelerated failure time (AFT) model and allowing for dependency between space and time via random effects (35). An additional extension of the spatially explicit model was performed by allowing the relation with the explanatory covariates to be spatially adaptive using a threshold conditional autoregressive (CAR) model (22), further extended to allow the inclusion of multiple threshold levels. All models were applied to prostate cancer survival data from the Louisiana SEER registry, which holds individual records linked to vital outcomes and is geocoded at the parish level.
Software for spatial survival
There are many R packages that can implement survival models, but only a few of them allow the inclusion of spatial effects. The spBayesSurv R package (39) implements proportional odds, proportional hazards and accelerated failure time models in a Bayesian approach using Markov chain Monte Carlo techniques. BayesX (40) is a software for estimating structured additive regression models with spatial random effects, which can be used for a Cox hazard regression models for continuous time survival analysis, in which the baseline hazard rate is estimated jointly with the other effects. It also allows time varying covariates, and any combination of left, right or interval censoring. For the estimation of the spatial random effects, BayesX uses Matern splines. R2BayesX is an R interface for BayesX (41).
The most popular software for modelling spatial survival is WinBUGS or OpenBUGS, which can implement the most widely used spatial survival models, such as Weibull distributed time to event survival data, accelerated failure times (AFT) and Cox proportional hazards models. In the next section we present an example analysis for Weibull distributed time to event survival data analysis.
Case study
For our application we consider the prostate cancer registry data from the SEER Louisiana registry for the years 2007 through 2010, which was used previously for the development of spatially explicit survival models (35,36). The data consists of 13,835 subjects, aggregated into 64 parishes in Louisiana. We selected only observations with complete dates available and excluded 437 subjects with survival time zero, considered unknown. For the analysis, we included 11,943 subjects with non missing covariates. The time to event outcome was the time to death from any causes as the prostate only cancer deaths were too infrequent (38). The follow-up cutoff date was December 31st, 2010. Any patient that died after the follow-up cut-off date was recoded to alive as of the cut-off date. A person alive at study termination or lost to follow-up at any time during the study was considered censored (42).
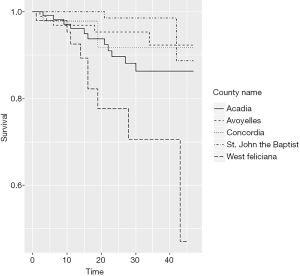
The use of this data is motivated by the high variability of the survival probabilities in the Louisiana parishes, as illustrated by the Kaplan-Meier survival curves for selected parishes displayed in Figure 1.
The following model implements a Bayesian survival analysis with Weibull distributed time to events.
The likelihood is specified using the zeros tricks in WinBUGS (34,43). We denote , where is the contribution to the likelihood of the individual. The likelihood can be written as a Poisson distribution as follows:
where is the time to event outcome vector and is the vector of parameters.
A constant C can be added to ensure that −li is positive, a, as follows:
The WinBUGS code for this model implementation is included in the Appendix 1. The code can be adapted for accelerated failure time models (AFT). A Bayesian spatial survival analysis using an AFT model for prostate cancer and sample WinBUGS code is provided by Zhang and Lawson (44).
Table 1 displays the coefficient estimates and 95% credible intervals. Black race (versus white and other races), stage (localized/regional versus distant based on SEER Historic Stage A), grade (1 and 2 versus 3 and 4) and increased age at diagnosis are associated with lower survival, while being married is associated with higher survival. The description of the variables can be found in the SEER Research Data description (42).
Table 1
| Variable | Estimate | 95% CI |
|---|---|---|
| Intercept | −7.04 | (−7.05, −6.72) |
| Black (versus white and other races) | 0.41 | (0.26, 0.57) |
| Married (versus not married) | −0.40 | (−0.55, −0.24) |
| Stage Localized/regional versus distant | 1.93 | (1.73, 2.13) |
| Grade (1 and 2 versus 3 and 4) | 0.22 | (0.059, 0.39) |
| Age at diagnosis | 0.71 | (0.64, 0.79) |
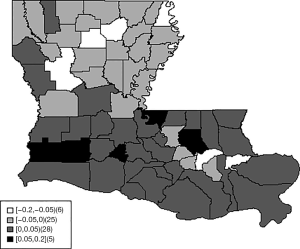
Figure 2 displays the sum of the uncorrelated and spatially correlated random effects.
The sum of random effects represents county specific changes of the log scale parameter log(λ) of the Weibull distribution. Higher random effects represent lower survival.
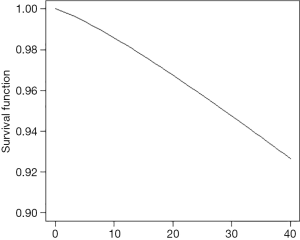
Counties with higher risk are mostly in the south-central part of the state. Figure 3 displays the spatially adjusted survival function, showing survival in all counties was higher than 90% after 40 months.
Conclusion
In this article, we provided a review of the spatial statistical models available for cancer survival, which is gaining prominence in the analysis of cancer data due to the availability of geographically reference data. The majority of the techniques use conditionally autoregressive (CAR) models for accounting for spatial variability, which is aligned with the Bayesian approach. Software for the spatial survival models include WinBUGS and R packages, although the algorithms can be implemented in a variety of software. A case study is included using the SEER prostate cancer data as an example of a spatial survival data analysis and coding.
Supplementary
Appendix 1 WinBUGS Code
model {
C<-100 # this just has to be large enough to ensure all phi[i]'s > 0
for(i in 1:N)
{
lambda[i]<-exp(beta0+beta1*black[i]+beta2*married[i]+beta3*distant[i]+beta4*grade34[i]+beta5*zage_dx[i]+V1[county[i]]+W[county[i]])
f[i]<-nu*lambda[i]*pow(time[i],nu-1)*exp(-pow(time[i],nu)*lambda[i])
S[i]<- exp(-pow(time[i],nu)*lambda[i])
#Loglikelihood function
L[i]<-death[i]*log(f[i])+(1-death[i])*log(S[i])
#poisson zero trick
zeros[i]<--0
phi[i]<- -L[i]+C
#modeldeviance[i]<- -2*L[i]
zeros[i]~dpois(phi[i])
}
nu<-exp(lognu)
beta0 ~dnorm(0.0,taubeta0)
sdbeta0~dunif(0,10)
beta1 ~dnorm(0.0,taubeta1)
sdbeta1~dunif(0,10)
beta2 ~dnorm(0.0,taubeta2)
sdbeta2~dunif(0,10)
beta3 ~dnorm(0.0,taubeta3)
sdbeta3~dunif(0,10)
beta4 ~dnorm(0.0,taubeta4)
sdbeta4~dunif(0,10)
beta5 ~dnorm(0.0,taubeta5)
sdbeta5~dunif(0,10)
taubeta0<-pow(sdbeta0,-2)
taubeta1<-pow(sdbeta1,-2)
taubeta2<-pow(sdbeta2,-2)
taubeta3<-pow(sdbeta3,-2)
taubeta4<-pow(sdbeta4,-2)
taubeta5<-pow(sdbeta5,-2)
lognu ~dnorm(0, 10)
###############################
for(i in 1:64){V1[i]~dnorm(0,tauV1)}
W[1:64]~car.normal(adj[],weights[],num[],tauW)
for(k in 1:sumNumNeigh)
{weights[k]<-1}
tauV1<-pow(sdV1,-2)
sdV1~dunif(0,10)
tauW<-1/(sdW*sdW)
sdW~dunif(0,10)
}
Supplementary
Acknowledgments
Funding: None.
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Peter Baade and Susanna Cramb) for the series “Spatial Patterns in Cancer Epidemiology” published in Annals of Cancer Epidemiology. The article has undergone external peer review.
Conflicts of Interest: Both authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/ace-19-32). The series “Spatial Patterns in Cancer Epidemiology” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Cutler SJ, Ederer F. Maximum utilization of the life table method in analyzing survival. J Chronic Dis 1958;8:699-712. [Crossref] [PubMed]
- U.S. Department of Health and Human Services. Healthy People 2020. 2014. Available online: https://www.healthypeople.gov. Accessed 09/18/2019.
- World Health Organization. Health Equity Monitor. Available online: https://www.who.int. Accessed November 10, 2019.
- Russell E, Kramer MR, Cooper HLF, et al. Residential Racial Composition, Spatial Access to Care, and Breast Cancer Mortality among Women in Georgia. J Urban Health 2011;88-29. [PubMed]
- Goungounga JA, Gaudart J, Colonna M, et al. Impact of socioeconomic inequalities on geographic disparities in cancer incidence: comparison of methods for spatial disease mapping. BMC Med Res Methodol 2016;16:136. [Crossref] [PubMed]
- Tian Y, Li J, Zhou T, et al. Spatially varying effects of predictors for the survival prediction of nonmetastatic colorectal Cancer. BMC Cancer 2018;18:1084. [Crossref] [PubMed]
- National Cancer Institute. Surveillance, Epidemiology and End Results Program. Available online: https://seer.cancer.gov/. Accessed November 16, 2019.
- Kleinbaum DG, Klein M. Survival Analysis A Self-Learning Text. Springer New York Dordrecht Heidelberg London; 2012.
- Gustafson P. Flexible Bayesian modelling for survival data. Lifetime Data Anal 1998;4:281-99. [Crossref] [PubMed]
- Ibrahaim J, Chen M, Sinha D. Bayesian Survival Analysis. New York: Springer; 2000.
- Banerjee S. Spatial survival models. Handbook of Spatial Epidemiology. New York: CRC Press; 2016.
- Besag J. Spatial interaction and the statistical analysis of lattice systems (with discussion). J R Stat Soc Series B Stat Methodol 1974;36:192-236.
- Besag J, York J, Mollié A. Bayesian image restoration, with two applications in spatial statistics. Ann Inst Stat Math 1991;43:1-20. [Crossref]
- Knorr-Held L, Besag J. Modelling risk from a disease in time and space. Stat Med 1998;17:2045-60. [Crossref] [PubMed]
- Zhou H, Lawson AB, Hebert JR, et al. Joint spatial survival modeling for the age at diagnosis and the vital outcome of prostate cancer. Stat Med 2008;27:3612-28. [Crossref] [PubMed]
- Lawson AB, Choi J, Zhang J. Prior choice in discrete latent modeling of spatially referenced cancer survival. Stat Methods Med Res 2014;23:183-200. [Crossref] [PubMed]
- Henderson R, Shimakura S, Gorst D. Modeling Spatial Variation in Leukemia Survival Data. J Am Stat Assoc 2002;97:965-72. [Crossref]
- Zhou H, Hanson T, Jara A, et al. Modeling county level breast cancer survival data using a covariate-adjusted frailty proportional hazards model. Ann Appl Stat 2015;9:43-68. [Crossref] [PubMed]
- Hanson TE, Jara A, Zhao L. A Bayesian Semiparametric Temporally-Stratified Proportional Hazards Model with Spatial Frailties. Bayesian Anal 2011;6:1-48. [PubMed]
- Short M, Carlin BP, Bushhouse S. Using hierarchical spatial models for cancer control planning in Minnesota (United States). Cancer Causes Control 2002;13:903-16. [Crossref] [PubMed]
- Berkson J, Gage RP. Survival curve for cancer patients following treatment. Am Statist Assoc 1959;47:501-15. [Crossref]
- Onicescu G, Lawson AB, Zhang J, et al. Spatially-explicit survival modeling with discrete grouping of cancer predictors. Spat Spatiotemporal Epidemiol 2019;29:139-48. [Crossref] [PubMed]
- Zhang Z. Parametric regression model for survival data: Weibull regression model as an example. Ann Transl Med 2016;4:484. [Crossref] [PubMed]
- Yu B, Tiwa RC. A Bayesian approach to mixture cure models with spatial frailties for population-based cancer relative survival data. Can J Stat 2012;40:40-54. [Crossref]
- Banerjee S, Carlin BP. Parametric spatial cure rate models for interval-censored time-to-relapse data. Biometrics 2004;60:268-75. [Crossref] [PubMed]
- Hurtado Rúa SM, Dey DK. A transformation class for spatio-temporal survival data with a cure fraction. Stat Methods Med Res 2016;25:167-87. [Crossref] [PubMed]
- Yakovlev AY. Threshold models of tumor recurrence. mathematical and computer modelling. Math Comput Model 1996;23:153-64. [Crossref]
- Chen MH, Ibrahim JG, Sinha D. A new Bayesian model for survival data with a surviving fraction. J Am Stat Assoc 1999;94:909-19. [Crossref]
- Li D, Wang X, Dey DK, et al. A flexible cure rate model for spatially correlated survival data based on generalized extreme value distribution and Gaussian process priors. Biom J 2016;58:1178-97. [Crossref] [PubMed]
- Cooner F, Banerjee S, Carlin BP, et al. Flexible cure rate modeling under latent activation schemes. J Am Stat Assoc 2007;102:560-72. [Crossref] [PubMed]
- Cooner F, Banerjee S, McBean MA. Modelling geographically referenced survival data with a cure fraction. Stat Methods Med Res 2006;15:307-24. [Crossref] [PubMed]
- Rondeau V, Schaffner E, Corbière F, et al. Cure frailty models for survival data: application to recurrences for breast cancer and to hospital readmissions for colorectal cancer. Stat Methods Med Res 2013;22:243-60. [Crossref] [PubMed]
- Price DL, Manatunga AK. Modelling survival data with a cured fraction using frailty models. Stat Med 2001;20:1515-27. [Crossref] [PubMed]
- Onicescu G, Lawson A. Bayesian cure-rate survival model with spatially structured censoring. Spat Stat 2018;28:352-64. [Crossref]
- Onicescu G, Lawson AB, Zhang J, et al. Bayesian Accelerated Failure Time Model for Space-Time Dependency in a Geographically Augmented Survival Model. Stat Methods Med Res 2017;26:2244-56. [Crossref] [PubMed]
- Onicescu G, Lawson AB, Zhang J, et al. Spatially explicit survival modeling for small area cancer data. J Appl Stat 2018;45:568-85. [Crossref] [PubMed]
- Gelfand AE, Diggle PJ, Fuentes M, et al. Handbook of Spatial statistics. CRC Press; 2010.
- Higdon D, editor. Space and Space-Time Modeling using Process Convolutions 2002; London: Springer London.
- Zhou H, Hanson T, Zhang J. spBayesSurv: fitting Bayesian spatial survival models using R. J Statist Softwr 2017. doi: arXiv:1705.04584
- Belitz C, Brezger A, Klein N, et al. BayesX Software for Bayesian Inference in Structured Additive Regression Models. Available online: http://wwwbayesxorg 2015.
- Umlauf N, Adler D, Kneib T, et al. Structured Additive Regression Models: An R Interface to BayesX. J Stat Software 2015;63:1-46. [Crossref]
- National Cancer Institute. {SEER} Research Data Record Description. Available online: https://seer.cancer.gov/data-software/documentation/seerstat/nov2018/TextData.FileDescription.pdf. Accessed November 24, 2019.
- Lunn D, Jackson C, Best N, et al. The BUGS Book: A Practical Introduction to Bayesian Analysis. Boca Raton, Florida: CRC Press, Chapman & Hall; 2013.
- Zhang J, Lawson A. Bayesian parametric accelerated failure time spatial model and its application to prostate cancer. J Appl Stat 2011;38:591-603. [Crossref] [PubMed]
Cite this article as: Fisher G, Lawson AB. Bayesian modeling of georeferenced cancer survival. Ann Cancer Epidemiol 2020;4:6.